为使其更直观,我们用图示法来说明。树用点来表示,植树的路线用线来表示,这样就把植树问题转化为一条非封闭或封闭的线上的“点数”与相邻两点间的线的段数之间的关系问题。
总结历年真题,可以将植树问题归纳为下面四种情形:
一、非封闭线的两端都有“点”时,“点数”=“段数”+1=总长/间隔+1。

常见题型如:一条河堤长420米,从头到尾每隔3米栽一棵树,要栽多少棵树?
二、非封闭线只有一端有“点”时,“点数”=“段数”。
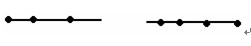
常见题型如:财院东门至文劳路的小路,长700米。要在小路一旁每隔2米栽一棵树,一共要栽多少棵树?
三、非封闭线的两端都没有“点”时,“点数”=“段数”-1。

常见题型如:两座楼房之间相距30米,每隔2米栽一棵树,需要种多少棵树?
四、封闭线上,“点数”=“段数”。
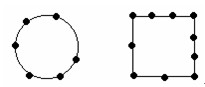
常见题型如:一个圆形水池的周长60米。如果在此水池边沿每隔3米放一盆花,那么一共能放多少盆花?
植树问题在现实生活中很常见,许多应用题都可以借助或归结为上述植树问题求解。
例1:在一条公路的两边植树,每隔3米种一棵树,从公路的东头种到西头还剩5棵树苗,如果改为每隔2.5米种一棵,还缺树苗115棵,则这条公路长多少米?( )
A.700 B.800 C.900 D.600
——『2008年陕西省公务员录用考试』
【答案:C】 解析:线型植树问题,这里需要注意的是公路两边都要种树。故总棵数=每边棵数×2。假设公路的长度为x米,则由题意可列方程:
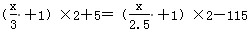 ,解得x=900,故选C。
,解得x=900,故选C。例2:一个四边形广场,它的四边长分别是60米、72米、84米和96米,现在要在四边上植树,四角需种树,而且每两棵树的间隔相等,那么至少要种多少棵树?
A. 22 B. 25 C. 26 D. 30
——『2009年江西省公务员录用考试』
【答案:C】 解析此题的关键点是“四角需种树”,欲使四个角都要种树,即是要求出60、72、84和96的最大公约数,为12,然后就是环形植树问题了,套用上面的第四种情况,所求棵数为:(60+72+84+96)/12=26。
例3:为了把2008年北京奥运办成绿色奥运,全国各地都在加强环保,植树造林。某单位计划在通往两个比赛场馆的两条路的(不相交)两旁栽上树,现运回一批树苗,已知一条路的长度是另一条路长度的两倍还多6000米,若每隔4米栽一棵,则少2754棵;若每隔5米栽一棵,则多396棵,则共有树苗( )。
——『2006年中央、国家机关公务员录用考试』
A.8500棵 B.12500棵 C.12596棵 D.13000棵
【答案:D】 解析:设两条路共长x米,共有树苗y棵,则x÷4+4=y+2754,x÷5+4=y-396,
解出y=13000(棵)。这里需要注意的是题目要求是在两条路上植树,每条路有两个边,故总棵数=段数+4。
例4:—人上楼,边走边数台阶。从一楼走到四楼,共走了54级台阶。如果每层楼之间的台阶数相同,他一直要走到八楼,问他从一楼到八楼一共要走多少级台阶?( )
A.126 B.120 C.114 D.108
——『2007年江西省公务员录用考试』
【答案:A】 解析:这是一道植树类问题的变形。需要注意的是从一楼到四楼实际上走的是三个楼层,每个楼层有台阶数54÷3=18(个),那么从一楼到八楼的台阶数就是:18×7=126(个)。
植树问题在现实生活中很常见,许多应用题都可以借助或归结为上述植树问题求解。
1. 在一段路边每隔50米埋设一根广告牌,包括这段路两端埋设的广告牌,共埋设了10根。这段路长多少米?
解:这是第(1)种情形,所以,“段数”=10-1=9。这段路长为50×(10-1)=450(米)。
2. 小王要到高层建筑的11层,他走到5层用了100秒,照此速度计算,他还需走多少秒?
解:因为1层不用走楼梯,走到5层走了4段楼梯,由此可求出走每段楼梯用100÷(5-1)=25(秒)。走到11层要走10段楼梯,还要走6段楼梯,所以还需25×6=150(秒)。
3. 一次检阅,接受检阅的一列彩车车队共30辆,每辆车长4米,前后每辆车相隔5米。这列车队共排列了多长?如果车队每秒行驶2米,那么这列车队要通过535米长的检阅场地,需要多少时间?
解:车队间隔共有30-1=29(个),每个间隔5米,所以,间隔的总长为(30-1)×5=145(米),
而车身的总长为30×4=120(米),故这列车队的总长为:(30-1)×5+30×4=265(米)。
由于车队要行265+535=800(米),且每秒行2米,
所以,车队通过检阅场地需要(265+535)÷2=400(秒)=6分40秒。
4. 下图是五个大小相同的铁环连在一起的图形。它的长度是多少?十个这样的铁环连在一起有多长?

解:如上图所示。关键是求出重叠的“环扣”数(每个长6毫米)。根据植树问题的第(3)种情形知,五个连在一起的“环扣”数为5-1=4(个),所以重叠部分的长为6×(5-1)=24(毫米),
又4厘米=40毫米,所以五个铁环连在一起长:40×5-6×(5-1)=176(毫米)。
同理,十个铁环连在一起的长度为:40×10-6×(10-1)=346(毫米)。
5. 甲乙两人一起攀登一个有300个台阶的山坡,甲每步上3个台阶,乙每步上2个台阶。从起点处开始,甲乙走完这段路共踏了多少个台阶?(重复踏的台阶只算一个)。
解:因为两端的台阶只有顶的台阶被踏过,根据已知条件,乙踏过的台阶数为300÷2=150(个),
甲踏过的台阶数为300÷3=100(个)。
由于2×3=6,所以甲乙两人每6个台阶要共同踏一个台阶,共重复踏了300÷6=50(个)。所以甲乙两人共踏了台阶150+100-50=200(个)。





